Correlation energy
Correlation energy is usually defined as the difference in energy between a higher level theory method, such as MP2 or CCSD, and the reference Hartree-Fock (HF). It is an important amount of the exact total energy that has major implications for prediction of properties or energy differences.
In ORCA, there are several methods implemented that compute or take this part into account, here we will discuss three of them: Møller–Plesset perturbation theory (MP2); double-hybrid DFT (DHDF) and coupled cluster (CC), using the singlet-triplet gap of methylene as a benchmark [Shavit1985]:
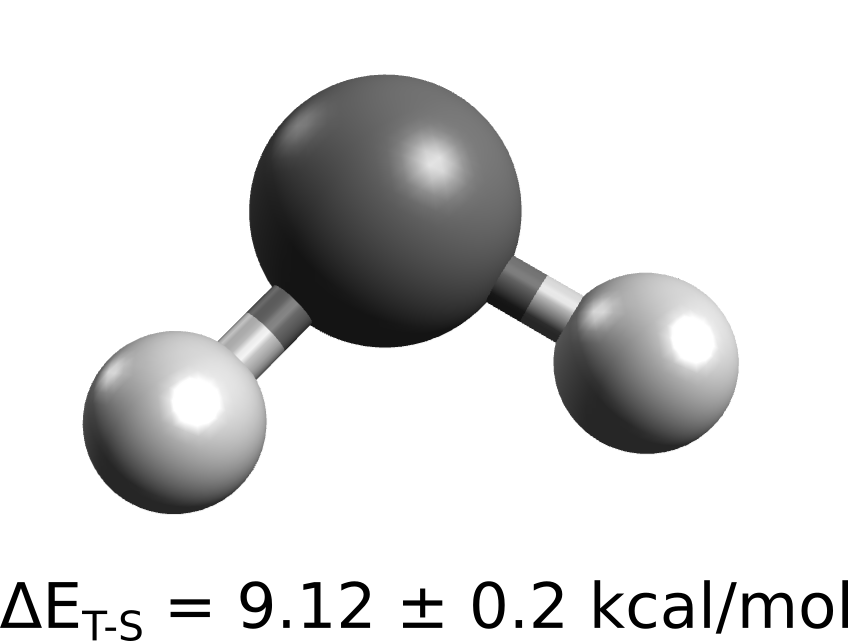
This is an unusual example where the ground triplet state is more stable than the singlet. Here the HF theory fails badly, and the the experimental properties were measured to good accuracy.
Møller–Plesset perturbation theory (MP2)
We start by computing the refence geometries for the singlet and triplet states using the DHDF B2PLYP, which is known to reproduce experimental geometries accurately [Grimme2006]:
!RI-B2PLYP DEF2-TZVPP DEF2-TZVPP/C OPT
* xyz 0 1
C 0.000000 0.000000 -0.092116
H -0.905815 0.000000 0.548403
H 0.905815 0.000000 0.548403
*
or:
!RI-B2PLYP DEF2-TZVPP DEF2-TZVPP/C OPT
* xyzFILE 0 3 guess_CH2.xyz
and the calculated bond angle found for the triplet is 134°, exactly the same found in the experiment [Shavit1985]
Now let's compute the adiabatic singlet-triplet energy difference using MP2 and the previously optimized structure for both singlets and triplets:
!MP2 DEF2-QZVPP
* xyz 0 1
C 0.000000 0.000000 -0.129289
H -0.859359 0.000000 0.566990
H 0.859359 0.000000 0.566990
*
or:
!MP2 DEF2-QZVPP
* xyz 0 3
C -0.000000 0.000000 0.056545
H -0.990707 0.000000 0.474072
H 0.990707 0.000000 0.474072
*
Important
It is important to stress here that these correlated methods depend strongly on the basis set size, and in principle one should aim for a larger basis when possible, that is why we are using the DEF2-QZVPP basis here.
You will see the MP2 header just after the SCF:
------------------------------------------------------------------------------
ORCA MP2
------------------------------------------------------------------------------
Freezing NCore=2 chemical core electrons
----------
MP2 ENERGY (disk based algorithm)
----------
Dimension of the basis ... 117
Memory devoted to MP2 ... 256 MB
Data format for buffers ... DOUBLE
Compression type for matrix containers ... UNCOMPRESSED
followed by details related to the necessary integrals:
-------------------------------
PARTIAL EXCHANGE TRANSFORMATION
-------------------------------
Transformation type ... one-operator
Generation of integrals (i,mue|j,nue) ... ON
Generation of integrals (mue,kappa|nue,tau)... OFF
Generation of integrals (i,mue|a,nue) ... OFF
Dimension of the basis ... 117
Number of internal MOs ... 3 ( 1- 3)
Pair cutoff ... 1.000e-11 Eh
and finally the correlation energy is printed (for the singlet):
-----------------------------------------------
MP2 CORRELATION ENERGY : -0.147755815 Eh
-----------------------------------------------
That is added to the SCF energy to then generate the final energy:
------------------------- --------------------
FINAL SINGLE POINT ENERGY -39.043423495766
------------------------- --------------------
Subtracting the triplet energy from the singlet at this level of theory one gets a \(\Delta E_{MP2} = 14.24 \hspace{3pt} kcal/mol\), which is about 5 kcal/mol higher in energy, but much better than the \(\Delta E_{HF} = 28.25 \hspace{3pt} kcal/mol\) obtained from HF theory.
Spin-component-scaled MP2 (SCS-MP2)
Another version of the MP2 theory is the spin-component-scaled MP2 (SCS-MP2, [Grimme2003]), that in general outperforms regular MP2. It can be easily used by calling:
!SCS-MP2 DEF2-QZVPP
* xyzFILE 0 1 CH2_optimized.xyz
or:
!SCS-MP2 DEF2-QZVPP
* xyzFILE 0 3 CH2_optimized.xyz
and a similar output is printed. In these cases, the energy difference we are calculating is \(\Delta E_{SCS-MP2} = 7.92 \hspace{3pt} kcal/mol\), even better than the regular MP2, but still missing.
Using the resolution of identity (RI)
The MP2 or SCS-MP2 calculations can be much accelerated using the resolution of identity approximation to the Coulomb integrals [Komornicki1993] by using:
!RI-MP2 DEF2-QZVPP DEF2-QZVPP/C
* xyzFILE 0 1 CH2_optimized.xyz
or:
!RI-SCS-MP2 DEF2-QZVPP DEF2-QZVPP/C
* xyzFILE 0 1 CH2_optimized.xyz
In this case, a special auxiliary basis is needed from the "/C" family of basis for correlated methods. A comprehensive list can be found in the ORCA manual, and if no corresponding basis is available, one can always use AUTOAUX to automatically generate one.
There is always an intrinsic error associated with any approximation, but here it is relatively small. As you can see, the final energy for the RI-MP2 on the singlet is:
------------------------- --------------------
FINAL SINGLE POINT ENERGY -39.054461324414
------------------------- --------------------
which is only tenths of microhartree far from the reference.
Note
The RIJDX and RIJCOSX approximations can also be used on the SCF part to further accelerate the calculation by using !RIJDX or !RIJCOSX in the main input.
The DLPNO scheme
The ORCA team has developed a special kind of approximation for these correlated methods over the years, called Domain-based Local Pair Natural Orbital (DLPNO) scheme.
The idea is that the correlation energy can be described in terms of electron pair energies, and these can be efficiently computed only within a certain domain of each pair. This makes these calculations much more efficient, and recover about 99% of the correlation energy.
In order to use this scheme for MP2:
!DLPNO-MP2 DEF2-QZVPP DEF2-QZVPP/C
* xyzFILE 0 1 CH2_optimized.xyz
or:
!DLPNO-SCS-MP2 DEF2-QZVPP DEF2-QZVPP/C
* xyzFILE 0 1 CH2_optimized.xyz
The output now has some extra printing, related to the localization of the orbitals:
------------------------------------------------------------------------------
ORCA ORBITAL LOCALIZATION
------------------------------------------------------------------------------
Input orbitals are from ... carb.gbw
Output orbitals are to ... carb.loc
Max. number of iterations ... 128
Localizations seeded randomly ... off
Convergence tolerance ... 1.000e-06
Treshold for strong local MOs ... 9.500e-01
Treshold for bond MOs ... 8.500e-01
[...]
followed by pre-screenings and the actual MP2 calculation runs:
----------------------------
Local MP2 Energy Calculation
----------------------------
Truncation parameters:
PAOOverlapThresh = 1.000e-08
TCutPNO = 1.000e-08
Spin component scaling .... not used
MP2 energy scaling factor .... 1.000
Formation of semicanonical amplitudes.
10% done.
20% done.
30% done.
40% done.
[...]
and the correlation energy is printed, as usual:
------------------------------------------------------
DLPNO-MP2 CORRELATION ENERGY: -0.158789484960 Eh
------------------------------------------------------
which is 99.99% close to the regular MP2 value.
Important
Calculations using DLPNO also always require a /C basis.
Double-hybrid density functionals (DHDF)
DFT already has a component of correlation energy to them, added by the exchange-correlation functional, but it was shown that by adding a certain amount of the MP2 correlation energy the results can be improved even further [Grimme2006].
These functionals with a MP2 component are named double-hybrids, for they include both HF exchange and MP2 correlation. They can be invoked, also with RI- and DLPNO- approximations. Using for instance with the B2PLYP functional these would be:
!B2PLYP DEF2-QZVPP
* xyzFILE 0 1 CH2_optimized.xyz
or:
!RI-B2PLYP DEF2-QZVPP DEF2-QZVPP/C
* xyzFILE 0 1 CH2_optimized.xyz
or:
!DLPNO-B2PLYP DEF2-QZVPP DEF2-QZVPP/C
* xyzFILE 0 1 CH2_optimized.xyz
The output follows a regular DFT calculation, with an MP2 calculation being done after the SCF. Finally all energies are added according the functional definition and the final energy is printed. For RI-B2PLYP, the singlet-triplet gap for methylene is \(\Delta E_{B2PLYP} = 11.73 \hspace{3pt} kcal/mol\), better than the simple MP2.
Double-hybrid spin-component-scaled density functionals (DSD-DF)
Following the same logic used for SCS-MP2, the different spin components of the MP2 energy can be scaled for the DHDF, which usually results in even better predictions [Grimme2011]. These functionals have DSD- in front of their name, for instance:
!DSD-PBEB95 DEF2-QZVPP
* xyzFILE 0 1 CH2_optimized.xyz
or:
!RI-DSD-PBEB95 DEF2-QZVPP DEF2-QZVPP/C
* xyzFILE 0 1 CH2_optimized.xyz
or:
!DLPNO-DSD-PBEB95 DEF2-QZVPP DEF2-QZVPP/C
* xyzFILE 0 1 CH2_optimized.xyz
Important
All methods presented so far are implemented with analytic gradients, which make them quite useful also for geometry optimizations!
Coupled cluster methods (CC)
One of the most accurate methods in quantum mechanics to get the correlation energy are so-called coupled cluster methods (CC), and in particular, the gold standard for accurate energies in single-reference problems is the CCSD(T) method.
However, that scales enormously with the number of electrons and can quickly become unpractical, limiting its range of application to about 20 atoms. In ORCA, it is possible to use the DLPNO scheme to significantly reduce the scaling of the problem, and nowadays real-life sized molecules with hundreds of atoms can be calculated [Neese2013a] [Neese2013b].
In order to compute the energies for our previous example, one can use:
!DLPNO-CCSD DEF2-QZVPP DEF2-QZVPP/C
* xyzFILE 0 1 CH2_optimized.xyz
and after the regular HF output, the Matrix Driven CI module starts (MDCI):
-------------------------------------------------------------------------------
ORCA-MATRIX DRIVEN CI
-------------------------------------------------------------------------------
Wavefunction type
-----------------
Correlation treatment ... CCSD
Single excitations ... ON
Orbital optimization ... OFF
Calculation of Z vector ... OFF
Calculation of Brueckner orbitals ... OFF
Perturbative triple excitations ... OFF
Calculation of F12 correction ... OFF
Frozen core treatment ... chemical core (2 el)
Reference Wavefunction ... RHF
Internal Orbitals: 1 ... 3 ( 3 MO's/ 6 electrons)
Virtual Orbitals: 4 ... 116 (113 MO's )
Number of AO's ... 117
Number of electrons ... 8
Number of correlated electrons ... 6
followed by the printings related to localization, screenings and integral transformations, after which the CCSD calculation starts:
------------------------------------------------
RHF COUPLED CLUSTER ITERATIONS
------------------------------------------------
Number of PNO amplitudes to be optimized ... 22277
Number of non-PNO amplitudes ... 76614
Untruncated number of regular amplitudes ... 76614
Iter E(tot) E(Corr) Delta-E Residual Time
0 -39.042828320 -0.146989446 0.000167865 0.017754515 4.35
*** Turning on DIIS ***
1 -39.056621207 -0.160782333 -0.013792887 0.014559282 4.14
Once it converges, as summary is printed with the different energy components and some diagnostics for this calculation:
----------------------
COUPLED CLUSTER ENERGY
----------------------
E(0) ... -38.895667683
E(CORR)(strong-pairs) ... -0.170828218
E(CORR)(weak-pairs) ... -0.000171190
E(CORR)(corrected) ... -0.170999408
E(TOT) ... -39.066667092
Singles Norm <S|S>**1/2 ... 0.022256446
T1 diagnostic ... 0.009086156
As you can see, the correlation here is more negative than for MP2, which is expected from a higher level method.
Warning
Please always check the T1 diagnostic value printed. A rule of thumb: for a diagnostic value larger than 0.02 the results are not to be trusted and the HF reference might be poor.
Note
There are many different coupled cluster and coupled pair methods that can be use in ORCA, check the ORCA manual for more details.
The predicted energy difference here is \(\Delta E_{CCSD} = 10.54 \hspace{3pt} kcal/mol\), better than the MP2, but still with some error. If one runs the same calculation using the even more accurate DLPNO-CCSD(T) instead, that difference goes down to \(\Delta E_{CCSD(T)} = 9.70 \hspace{3pt} kcal/mol\), which is almost exactly like the experimental value!
Extrapolation to the CBS limit
As mentioned before in the MP2 section, these methods require large basis set to be really accurate, and their true power show up only when close to the basis set (CBS) limit. Even so, one does not need to use an immense basis to get there, it is also possible to extrapolate the CBS from lower basis set calculations.
Using these extrapolation schemes with ORCA is easy. For instance, if you want to compute the DLPNO-CCSD(T) energy close to the CBS, one can use:
!DLPNO-CCSD(T) EXTRAPOLATE(3) cc-pVQZ/C
* xyzFILE 0 1 CH2_optimized.xyz
The EXTRAPOLATE(3) keyword here means that three calculations using the basis set from the family cc-pVxZ (where x is D, T and then Q) will be done and the CBS results will be extrapolated from that.
Note
The /C basis is not automatically chosen, so it is best to use the one corresponding to the largest basis. Please check the ORCA manual for a complete description of the EXTRAPOLATE possibilities.
Going back to methylene triplet-singlet gap, the extrapolated energy difference is \(\Delta E_{CCSD(T)-CBS} = 9.26 \hspace{3pt} kcal/mol\), which is actually within the experimental error.
Here is a table summarizing the calculated results. It is clear that the error get smaller as the correlated method gets more and more accurate:
Method |
\(\Delta E_{TS}\) |
Error |
|---|---|---|
HF |
28.25 |
19.13 |
B3LYP |
11.74 |
2.62 |
MP2 |
14.24 |
5.11 |
SCS-MP2 |
7.92 |
-1.22 |
RI-B2PLYP |
11.73 |
2.60 |
RI-DSD-PBEB95 |
11.63 |
2.50 |
DLPNO-CCSD |
10.54 |
1.42 |
DLPNO-CCSD(T) |
9.70 |
0.58 |
DLPNO-CCSD(T)-CBS |
9.26 |
0.14 |
Experiment [Shavit1985] |
9.12 |
± 0.2 |