Thermodynamics
If you have successfully done a Vibrational frequencies calculation, now you have access to the thermodynamic functions such as enthalpy (\(H\)), entropy (\(S\)) and the Gibbs free energy (\(G\))!
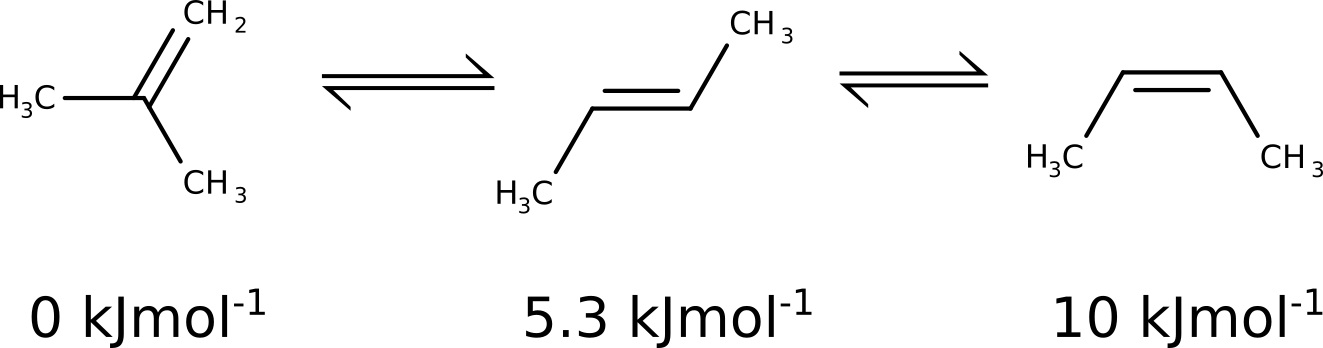
Let's follow an example and use this to predict the relative energy ordering of some butadiene isomers.
using the following keywords and the geminal isomer as an example:
!B3LYP DEF2-TZVP OPT FREQ
* XYZFILE 0 1 gem-butene.xyz
Thermodynamic functions
Assuming you had !FREQ on the input, immediately after the frequencies and normal modes, one will see that the thermochemistry section starts:
--------------------------
THERMOCHEMISTRY AT 298.15K
--------------------------
Temperature ... 298.15 K
Pressure ... 1.00 atm
Total Mass ... 56.11 AMU
Note
These properties will be computed for a given temperature and pressure, assuming a gas-phase molecule and using statistical mechanics. For thermodynamics in solution, check the Implicit Solvation Models section.
Inner energy
The first function is the inner energy (\(U\)), that is computed following the output:
------------
INNER ENERGY
------------
The inner energy is: U= E(el) + E(ZPE) + E(vib) + E(rot) + E(trans)
E(el) - is the total energy from the electronic structure calculation
= E(kin-el) + E(nuc-el) + E(el-el) + E(nuc-nuc)
E(ZPE) - the the zero temperature vibrational energy from the frequency calculation
E(vib) - the the finite temperature correction to E(ZPE) due to population
of excited vibrational states
E(rot) - is the rotational thermal energy
E(trans)- is the translational thermal energy
Summary of contributions to the inner energy U:
Electronic energy ... -157.17473665 Eh
Zero point energy ... 0.10741046 Eh 67.40 kcal/mol
Thermal vibrational correction ... 0.00247510 Eh 1.55 kcal/mol
Thermal rotational correction ... 0.00141627 Eh 0.89 kcal/mol
Thermal translational correction ... 0.00141627 Eh 0.89 kcal/mol
-----------------------------------------------------------------------
Total thermal energy -157.06201854 Eh
The Electronic energy is what you get from the FINAL SINGLE POINT ENERGY, then the Zero-Point Energy (ZPE) is calculated, together with the thermal correction, which has to do with the rotational, vibrational and translational degrees of freedom.
The Total correction is amount the of energy you have to add to your FINAL SINGLE POINT electronic energy to convert \(E_{el}\) into \(U\).
Enthalpy
Then the calculation of the enthalpy. That is simply \(U + k_BT\):
--------
ENTHALPY
--------
The enthalpy is H = U + kB*T
kB is Boltzmann's constant
Total free energy ... -157.06201854 Eh
Thermal Enthalpy correction ... 0.00094421 Eh 0.59 kcal/mol
-----------------------------------------------------------------------
Total Enthalpy ... -157.06107433 Eh
Again, the Thermal Enthalpy correction is what one has to add to \(U\) to compute \(H\).
Entropy
The entropy term follows:
-------
ENTROPY
-------
The entropy contributions are T*S = T*(S(el)+S(vib)+S(rot)+S(trans))
S(el) - electronic entropy
S(vib) - vibrational entropy
S(rot) - rotational entropy
S(trans)- translational entropy
The entropies will be listed as mutliplied by the temperature to get
units of energy
Electronic entropy ... 0.00000000 Eh 0.00 kcal/mol
Vibrational entropy ... 0.00394490 Eh 2.48 kcal/mol
Rotational entropy ... 0.01155172 Eh 7.25 kcal/mol
Translational entropy ... 0.01805279 Eh 11.33 kcal/mol
-----------------------------------------------------------------------
Final entropy term ... 0.03354941 Eh 21.05 kcal/mol
with its different components and a Final entropy term that is already multiplied by the temperature, the \(TS\) term that is latter used for the free energy.
Gibbs free energy
Finally, the free energy term is printed:
-------------------
GIBBS FREE ENERGY
-------------------
The Gibbs free energy is G = H - T*S
Total enthalpy ... -157.06107433 Eh
Total entropy correction ... -0.03354941 Eh -21.05 kcal/mol
-----------------------------------------------------------------------
Final Gibbs free energy ... -157.09462374 Eh
For completeness - the Gibbs free energy minus the electronic energy
G-E(el) ... 0.08011291 Eh 50.27 kcal/mol
The last term, G-E(el) is exactly what you have to add to your electronic energy to transform \(E_{el}\) into \(G^o\) at a given temperature and pressure.
Note
This G-E(el) only depends on the geometry and frequencies, and thus can be computed in a lower level method, such as DFT, and later combined with the \(E_{el}\) of a higher level method, such as DLPNO-CCSD(T) to achieve a very good prediction of the \(G^o\)!
Comparison to experiment
By taking the Gibbs free energy values directly from the DFT results:
!B3LYP DEF2-TZVP OPT FREQ
* XYZFILE 0 1 butene.xyz
the predicted energy differences are \(1.02\) \(kJmol^{-1}\) and \(5.99\) \(kJmol^{-1}\), which captures the differences between cis and trans, but is certainly not good with respect to the most stable geminal isomer.
This can be made better by computing the electronic energy \(E_{el}\) at a high-quality DLPNO-CCSD(T) level, given by the FINAL SINGLE POINT ENERGY:
!DLPNO-CCSD(T) aug-cc-pVTZ AUTOAUX RIJCOSX
* XYZFILE 0 1 butene_optimized_DFT.xyz
and adding the G-E(el) term from DFT to form a better final Gibbs free energy, and the results then are:
Compound |
DFT |
CCSD(T)+DFT |
Exp. |
|---|---|---|---|
1 |
0 |
0 |
0 |
2 |
1.02 |
4.45 |
5.3 |
3 |
5.99 |
9.11 |
10.0 |
Thermodynamics at different temperatures
To compute these thermodynamic properties at different temperatures, or at several, one can use:
%FREQ TEMP 77, 298, 330, 450 END
and the thermodynamic functions will be separated by the headers:
--------------------------
THERMOCHEMISTRY AT 77K
--------------------------
[...]
--------------------------
THERMOCHEMISTRY AT 298K
--------------------------
[...]
and so on.
Changing the temperature after the calculation
If you want to compute thermodynamic functions after you calculation has already finished, that can be done setting a simple input such as:
!PRINTTHERMOCHEM
%GEOM
INHESSNAME "basename.hess"
END
%FREQ TEMP 290, 295, 300
END
* XYZFILE 0 1 geometry.xyz
as one can save a lot of time from recalculations.
Note
One could use this to also include isotopic effects, by changing the masses in the basename.hess file and recomputing the thermodynamics (see Kinectic Isotope Effects).
Starting structures
gem-butene
C -1.43336 0.99760 -0.11833
C -0.17392 0.62436 -0.39435
C 0.14450 -0.70205 -1.02166
C 1.00254 1.50776 -0.09468
H 0.65348 -0.55631 -1.97995
H -0.75651 -1.29570 -1.20886
H 0.79819 -1.28546 -0.36521
H -2.27870 0.35250 -0.33839
H -1.65494 1.95886 0.33562
H 1.55177 1.73378 -1.01439
H 0.69898 2.45896 0.35516
H 1.68283 1.00994 0.60389
trans-butene
C 1.30292 0.51517 0.05694
C -0.04707 -0.10202 0.22754
H 1.76922 0.66709 1.03514
H 1.25468 1.48282 -0.45237
H 1.94420 -0.14853 -0.53097
C -1.18840 0.46276 -0.19477
C -2.53838 -0.15441 -0.02414
H -3.00427 -0.30734 -1.00238
H -3.17998 0.50979 0.56286
H -2.49026 -1.12154 0.48617
H -0.07366 -1.06762 0.72803
H -1.16180 1.42834 -0.69529
cis-butene
C 1.48629 -0.48153 0.16062
C 0.03276 -0.80512 0.28503
H 1.68200 0.56889 -0.06324
H 1.92979 -1.08298 -0.63914
H 1.99954 -0.72748 1.09552
C -1.01110 0.03009 0.16420
H -0.18277 -1.85160 0.49931
C -0.98494 1.49624 -0.12334
H -2.00868 -0.39072 0.28765
H -1.47672 2.03930 0.68986
H 0.02271 1.90131 -0.23449
H -1.53322 1.69981 -1.04849