Kinectic Isotope Effects
Kinetic isotope effects (KIE) are changes in reaction rates caused by a change in a given isotope in a molecule. That is caused due to the difference in mass, that affects vibrational frequencies and/or tunneling probabilities.
It is an effect often exploited to investigate reaction mechanisms, when there is bond breaking or forming to an atom that can be substituted by an isotope. These KIE are somehow predictable, depending on the mass ratios, and thus can be used to validate proposed mechanisms.
We can also use ORCA to make a quantum-mechanical prediction of the KIE, and use these to further investigate chemical reactivity. Let's try to predict the KIE in a H-atom abstraction of methane by the hydroxyl radical, that was measured with high accuracy in gas phase [Tully1993]:
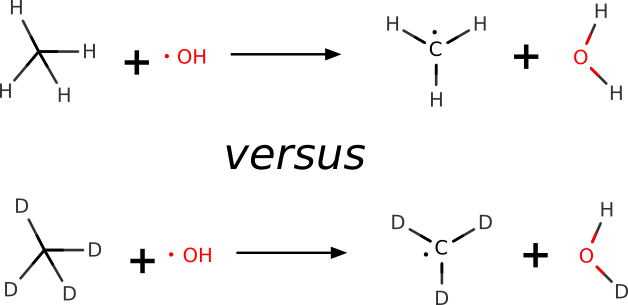
KIE in a H-atom abstraction
In order to predict the KIE, one has first to find the transition state involved in this reaction. The "Finding transition states with NEB-TS" section already explains the details on how to do that. It basically involves optimizing the reactant and the products:
!B3LYP DEF2-SVP D3 OPT FREQ
%FREQ TEMP 293 END
* xyzFILE 0 2 reactants.xyz
and:
!B3LYP DEF2-SVP D3 OPT FREQ
%FREQ TEMP 293 END
* xyzFILE 0 2 products.xyz
together with the NEB-TS method to find the transition state. Here we use the TEMP flag under %FREQ, to compute the Thermodynamics at the same temperature where it was measured, i.e. 293 K.
The NEB-TS calculation is then invoked by:
!B3LYP DEF2-SVP D3 FREQ ZOOM-NEB-TS
%FREQ TEMP 293 END
%NEB NEB_END_XYZFILE "products_optimized.xyz" END
* xyzFile 0 2 reactants_optimized.xyz
This is a particular tricky case, however small, and in order to help with the optimization we chose the ZOOM-NEB-TS method.
HAVE TO FINISH HERE
The TS found then is:
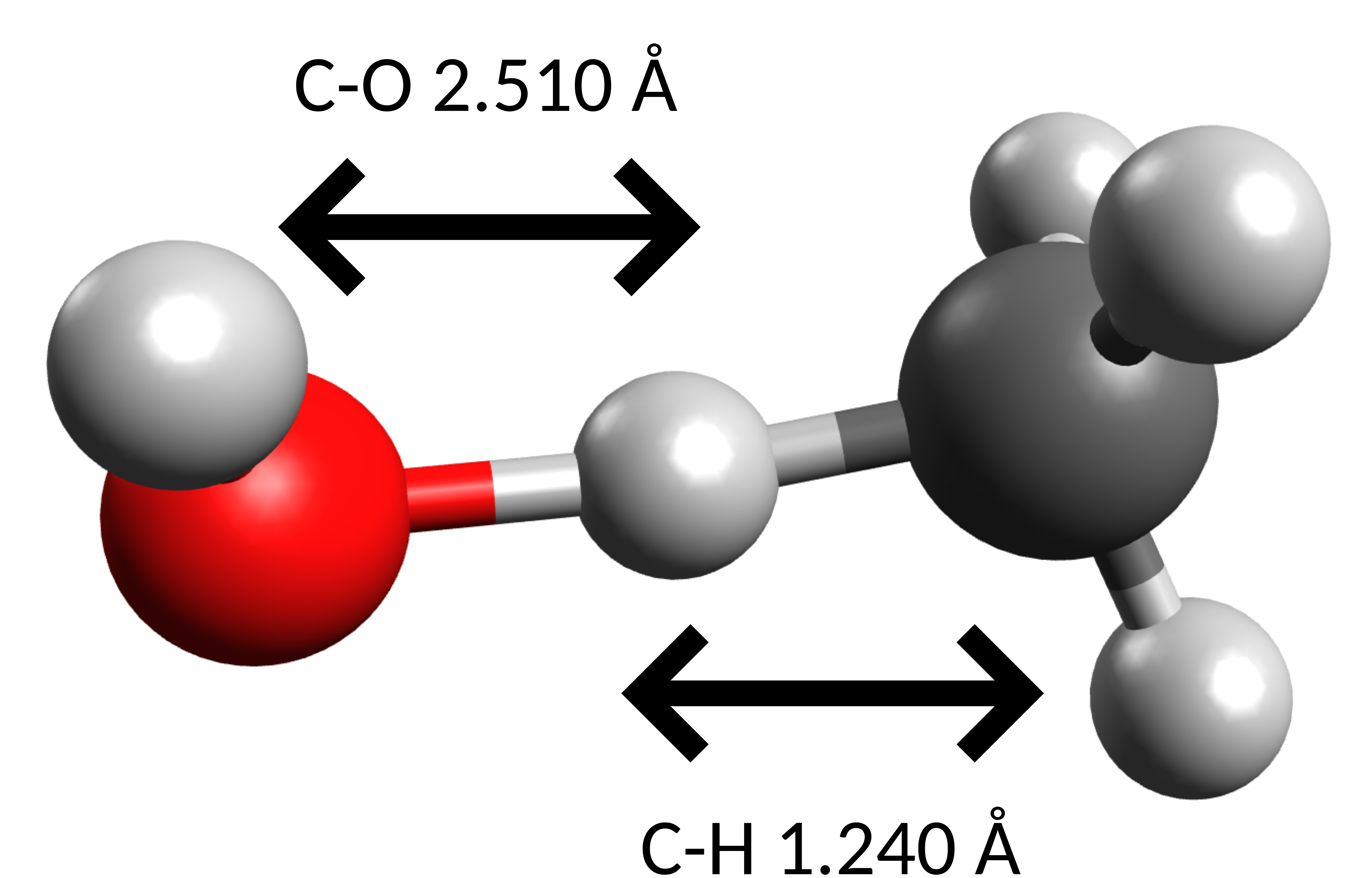
which is the rather obvious pathway for an H-atom abstraction, and presents a single negative frequency of \(-1070 cm^{-1}\) along the O-H-C coordinate.
Using the previously explained method in the Thermodynamics and Calculating accurate energy barriers sections, the \(\Delta G_H^{\ddagger}\) calculated is \(10.11\) \(kJmol^{-1}\).
Changing the isotopes
Now, we need to compute the \(\Delta G^{\ddagger}\) for the reaction involving the deuterated methane. Assuming that the bond lengths and electronic energies are the same, which is very well true for such a small change in the mass, one needs only to recompute the vibrational corrections to the Gibbs free energy.
That can be easily done using the !PRINTTHERMOCHEM flag, also already presented in the Thermodynamics section, without the need to repeat the whole optimization plus NEB-TS process.
In this case, we only need to add the mass of the new isotope on the geometry section of the input, such as:
!PRINTTHERMOCHEM
%GEOM INHESSNAME "R.hess" END
%FREQ TEMP 293 END
* xyz 0 2
C -2.411352 1.128722 0.029849
H -1.342943 1.352019 -0.097229 M 2.00141
H -2.853386 0.899279 -0.950538 M 2.00141
H -2.919524 2.002716 0.462768 M 2.00141
H -2.541362 0.264118 0.697923 M 2.00141
O 1.133678 1.702618 0.011070
H 0.792228 1.085478 0.693266
*
for both the reactant and the TS. The M 2.00141 after the coordinates of the hydrogens indicate that these atoms now should have the mass of \(2.00141 amu\), corresponding to a deuterium atom. Of course, this is atom-specific and the hydroxyl radical stays the same.
Now, a new correction to transform the electronic energy into \(G^o\) is printed, and the new \(\Delta G_D^{\ddagger}\) can be obtained, with a value of \(14.90\) \(kJmol^{-1}\).
Calculating the KIE
The origin of the KIE is related to a change on the Zero Point Energy (ZPE) of the system, that is affected when the vibrational frequencies are lowered or increased due to the mass change.
In our case, the heavier deuterium lowers the vibrational frequencies, thus lowering the ZPE and altering the energy barrier:
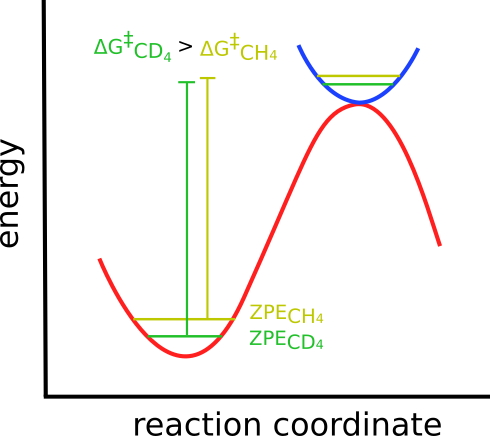
The reactant ZPE is usually more affected than the TS, since it is more strongly bound, and the changes in the \(\Delta G^{\ddagger}\) are uneven.
With the new barriers, come the new rates and the KIE is then computed as the ratio of \(k_H / k_D\), that in terms of free energies is given by:
Using both free energy barriers calculated, this ratio is predicted to be \(7.41\), well within the experimental value of \(6.75 \pm 0.83\). That is a high value for a primary isotope effect, but in this case it makes sense if one considers that the transition state is directly dependent on the bonds with the hydrogen atom.
Important
By simply computing the KIE in terms of changes on the energy barriers like that, we are ignoring tunneling effects. Those can be quite important, and sometimes need to be included using one of the many different approaches, eg. [Aquilanti2019].
Starting structures
Reactant
C -2.42007 1.14475 0.00503
H -1.37176 1.42602 -0.24888
H -2.95035 0.87504 -0.97240
H -2.97696 2.02414 0.50780
H -2.39461 0.26127 0.72431
O 1.11295 1.79481 -0.12688
H 0.85814 0.90892 0.95813
Product
C -2.640806 0.931381 0.002030
H 0.593417 1.397564 -0.537054
H -3.426646 1.364904 -0.619289
H -1.670863 1.425720 0.075351
H -2.839810 0.009183 0.550600
O 0.590809 2.120231 0.105838
H 0.558140 1.654177 0.952824